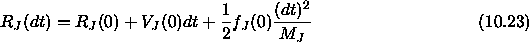Each inertia tensor is diagonalized by a rotational transformation to the body coordinate system:
The transformation matrix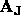 
is used to initialize rotational
variables such that 
=
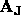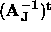. Values for the
body-frame coordinates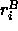 
of group elements are obtained by
The net force and torque acting on each body are determined by summing the force and torque acting on each of its constituent atoms. Center-of-mass variables are initialized with a two-step process. The initial center-of-mass velocities are determined from the atom properties VX,VY,VZ:
These velocities are then used to advance the center-of-mass coordinates
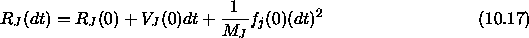
The more stable Euler-Cayley
parameters (also referred to as quaternions)
are used as rotational variables instead of the Euler angles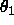 
,
, 
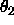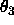(cf. Goldstein 1980). They are defined in
Eq. 2.1.
The quaternions
are initialized using a first-order approximation to their equation of
motion:
where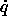 
is the four-vector (
,
,
,
),
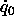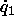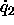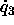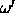is the four-vector (0,
,
,
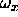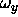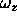), and
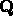is the matrix that gives their time evolution:
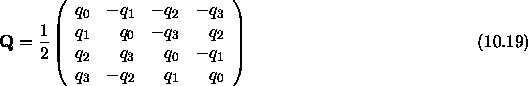
Thus one obtains
The initial angular velocity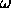 
follows directly from the
initial angular momentum, which is determined by
where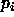 
is the momentum of the 
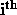atom of the rigid body.
The initial half-step advanced angular momentum can be expressed as
and the first advancement of the center-of-mass coordinates can be written as
