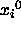 are subjected to the SHAKE method.
Then the system gets the initial velocities
are subjected to the SHAKE method.
Then the system gets the initial velocities 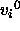 . Next,
the program prints the energy of the initial coordinates. A two-step
method is used to obtain the coordinates
. Next,
the program prints the energy of the initial coordinates. A two-step
method is used to obtain the coordinates 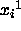 :
:
X-PLOR makes use of a third-order
finite difference approximation in dt
(Brünger, Brooks, and Karplus 1984).
First, the initial coordinates 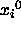 are subjected to the SHAKE method.
Then the system gets the initial velocities
are subjected to the SHAKE method.
Then the system gets the initial velocities 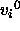 . Next,
the program prints the energy of the initial coordinates. A two-step
method is used to obtain the coordinates
. Next,
the program prints the energy of the initial coordinates. A two-step
method is used to obtain the coordinates 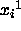 :
:
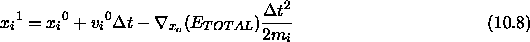
IF SHAKE constraints are present,
the SHAKE method is applied to 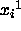 with respect to
with respect to 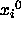 .
.
Iteration from step n to step n+1 causes
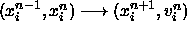 .
The algorithm computes the forces
.
The algorithm computes the forces 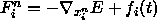 .
The algorithm then computes
.
The algorithm then computes
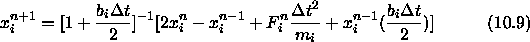
If required, the SHAKE method
is applied to 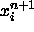 with
with 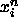 as the
reference set. Finally, the velocities at this step are computed:
as the
reference set. Finally, the velocities at this step are computed:

(The velocities do not enter the equations to compute the
trajectory 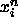 .) In case of
zero friction coefficients
.) In case of
zero friction coefficients 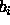 , this algorithm
reduces to the three-step Verlet method
(Verlet 1967).
, this algorithm
reduces to the three-step Verlet method
(Verlet 1967).