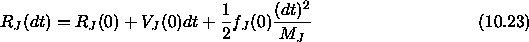Each inertia tensor is diagonalized by a rotational transformation to the body coordinate system:

The transformation matrix  is used to initialize rotational
variables such that
is used to initialize rotational
variables such that 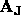 =
=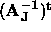 . Values for the
body-frame coordinates
. Values for the
body-frame coordinates 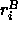 of group elements are obtained by
of group elements are obtained by

The net force and torque acting on each body are determined by summing the force and torque acting on each of its constituent atoms. Center-of-mass variables are initialized with a two-step process. The initial center-of-mass velocities are determined from the atom properties VX,VY,VZ:

These velocities are then used to advance the center-of-mass coordinates
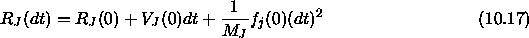
The more stable Euler-Cayley
parameters (also referred to as quaternions)
are used as rotational variables instead of the Euler angles 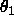 ,
,
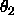 ,
, 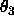 (cf. Goldstein 1980). They are defined in
Eq. 2.1.
The quaternions
are initialized using a first-order approximation to their equation of
motion:
(cf. Goldstein 1980). They are defined in
Eq. 2.1.
The quaternions
are initialized using a first-order approximation to their equation of
motion:

where 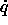 is the four-vector (
is the four-vector ( ,
,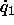 ,
,
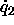 ,
,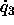 ),
),
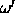 is the four-vector (0,
is the four-vector (0,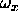 ,
,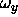 ,
,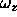 ), and
), and
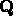 is the matrix that gives their time evolution:
is the matrix that gives their time evolution:
Thus one obtains

The initial angular velocity  follows directly from the
initial angular momentum, which is determined by
follows directly from the
initial angular momentum, which is determined by

where  is the momentum of the
is the momentum of the  atom of the rigid body.
The initial half-step advanced angular momentum can be expressed as
atom of the rigid body.
The initial half-step advanced angular momentum can be expressed as

and the first advancement of the center-of-mass coordinates can be written as