Next: 3D NOE-NOE Example Up: Distance Restraints Previous: Dihedral Angle Restraints

Distance Symmetry Restraints

The symmetry function restrains distance differences between pairs of ASSIgn statements. The distance pairs should be entered as follows:

assign (segid a and resid 1 and name ca)                 {* First distance.*}
       (segid b and resid 10 and name ca)   0.0 0.1 0.1

                                                        {* Second distance.*}
assign (segid a and resid 10 and name ca)
       (segid b and resid 1 and name ca)   0.0 0.0 0.0

This particular example restrains the signed difference between the first and second distance to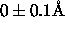

. The values of r,

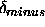, and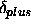

for the second distance are not used by the program.

The list of symmetry-related intermonomer distance differences for a dimeric protein can be generated automatically by the following script, which produces a file ``symrest.tbl":

                                   {* Name of the distance restraints file.*}
set display=symrest.tbl end

                                      {* Get number of residues in monomer.*}
vector do (store1 = decode(resid)) (segid a and name ca)
vector show min (store1) (segid a and name ca)
evaluate ($first_residue = $result)
vector show max (store1) (segid a and name ca)
evaluate ($last_residue = $result)

for $id in id (name ca and segid a) loop res1
    vector show element (resid) (id $id)
    evaluate ($resid1 = decode($result))
    evaluate ($resid2 = $last_residue - $resid1 + $first_residue)
    if ($resid2 > $resid1) then
        display ! distance pair $resid1 $resid2
        display assign (resid $resid1 and name ca and segid a)
        display        (resid $resid2 and name ca and segid b) 0 0 0
        display assign (resid $resid1 and name ca and segid b)
        display        (resid $resid2 and name ca and segid a) 0 0 0 
    end if
end loop res1

The resulting distance difference list will restrain the distance differences to 0; i.e., it will attempt to produce a perfectly symmetric arrangement of the dimer.

The next example shows how one would actually use the symmetry restraints:

noe
  class      symm @symmetry.tbl

  potential  symm symmetry
  scale      symm 1.0                           
  sqconstant symm 1.0
  sqexponent symm 2
  soexponent symm 1
  rswitch    symm 0.5
  sqoffset   symm 0.0
  asymptote  symm 1.0
end

Note that these symmetry distance restraints are more stringent than the non-crystallographic symmetry restraints described in Section 16.1. The distance symmetry implies twofold symmetry whereas the non-crystallographic symmetry restraints simply restrain the monomers to be nearly superimposable without specification of a specific operation between the monomers. The distance symmetry restraints are, however, less stringent than the strict non-crystallographic symmetry (Section 16.2), as the latter requires explicit specification of the symmetry operation. The distance symmetry restraints allow the separation between the monomers to be a self-adjusting parameter. (For further reading, see Nilges and Brünger 1991.)

Web Manager
Sat Mar 11 09:37:37 PST 1995