Equipe de chimie théorique,
Institut nancéien de chimie moléculaire,
UMR CNRS/UHP 7565,
Université Henri Poincaré,
BP 239,
54506 Vand
This feature has been contributed to NAMD by the following authors:
Surjit B. Dixit and Christophe Chipot
Equipe de chimie théorique,
Institut nancéien de chimie moléculaire,
UMR CNRS/UHP 7565,
Université Henri Poincaré,
BP 239,
54506 Vanduvre-lès-Nancy cedex, France
A method to perform alchemical free energy perturbation (FEP)
[21,4,20,19,12,9,13,8] within NAMD has now been implemented.
Within FEP, the difference in free energy between two states,
![]() and
and ![]() , is expressed by:
, is expressed by:
| (3) |
wherein ![]() is the Boltzmann constant,
is the Boltzmann constant, ![]() is the kinetic temperature,
and
is the kinetic temperature,
and
![]() and
and
![]() are the Hamiltonians characteristic of states
are the Hamiltonians characteristic of states ![]() and
and ![]() , respectively.
, respectively.
![]() denotes an ensemble average over configurations
representative of the initial state,
denotes an ensemble average over configurations
representative of the initial state, ![]() .
In practice, the transformation between the two thermodynamic states
is replaced by a series of transformations between non-physical,
intermediate states along a pathway that connects
.
In practice, the transformation between the two thermodynamic states
is replaced by a series of transformations between non-physical,
intermediate states along a pathway that connects ![]() to
to ![]() .
This pathway is characterized by a variable, referred to as
``coupling parameter'', [4,13,11]
.
This pathway is characterized by a variable, referred to as
``coupling parameter'', [4,13,11]
![]() , that makes the free energy
a continuous function of this parameter between
, that makes the free energy
a continuous function of this parameter between ![]() and
and ![]() :
:
![\begin{displaymath}
\Delta A_{a \rightarrow b} = -k_B T \ \sum_{k = 1}^N \ln
\le...
...cal H}({\bf r}, {\bf p}; \lambda_k)}
{k_B T}\right]
\right>_k
\end{displaymath}](img245.gif) |
(4) |
Here, ![]() stands for the number of intermediate states, or ``windows''
between the initial and the final states.
stands for the number of intermediate states, or ``windows''
between the initial and the final states.
In a typical FEP setup involving the transformation
of one chemical species into another one in the course
of the simulation, the atoms in the molecular topology can be
classified into three groups. A group of atoms that do not change
during the simulation -- e.g.the environment,
the atoms describing the initial state, ![]() , of the system, and, last, the
atoms that correspond to the final state,
, of the system, and, last, the
atoms that correspond to the final state, ![]() , at the end of the
alchemical transformation.
The atoms representative of state
, at the end of the
alchemical transformation.
The atoms representative of state ![]() do not interact with those of state
do not interact with those of state ![]() throughout the
entire molecular dynamics simulation.
Such a setup, in which atoms of both the initial and the
final states of the system are present in the molecular topology file -- i.e.
the psf file -- is characterisitic of the so-called ``dual topology''
protocol. [2]
The hybrid Hamiltonian of the system, which is a function of the
coupling parameter
throughout the
entire molecular dynamics simulation.
Such a setup, in which atoms of both the initial and the
final states of the system are present in the molecular topology file -- i.e.
the psf file -- is characterisitic of the so-called ``dual topology''
protocol. [2]
The hybrid Hamiltonian of the system, which is a function of the
coupling parameter ![]() , that smoothly connects state
, that smoothly connects state ![]() to state
to state ![]() , is calculated as:
, is calculated as:
| (5) |
where ![]() is the Hamiltonian of the group of atoms representative
of the initial state,
is the Hamiltonian of the group of atoms representative
of the initial state, ![]() , and
, and ![]() characterizes the final state,
characterizes the final state,
![]() .
.
![]() is the Hamiltonian for those atoms that do not undergo any
transformation during the MD simulation.
is the Hamiltonian for those atoms that do not undergo any
transformation during the MD simulation.
In the present implementation of FEP in NAMD, we employ a hamiltonian
scaling procedure as is done in the ``dual topology''
approach, [15] i.e.instead
of scaling the non-bonded parameters of states ![]() and
and ![]() ,
namely the net atomic charges, together with the Lennard-Jones parameters,
as a function of the coupling parameter,
,
namely the net atomic charges, together with the Lennard-Jones parameters,
as a function of the coupling parameter, ![]() :
:
| (6) | |||
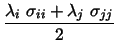 |
where ![]() and
and ![]() take the value of
take the value of ![]() or
or ![]() ,
depending upon state
,
depending upon state ![]() or
or ![]() , to which
, to which ![]() or
or ![]() belong.
belong.
For instance, in a transformation involving the mutation of an
alanine side chain into that of glycine, using the FEP, the topology
of both the methyl group borne by the C![]() in alanine,
and the hydrogen of glycine co-exist throughout the simulation
(see Figure 5).
in alanine,
and the hydrogen of glycine co-exist throughout the simulation
(see Figure 5).
![\includegraphics[width=14.5cm]{figures/dual_top}](img264.gif) |
The charge and Lennard-Jones parameters of the alanine and
the glycine side chains
are defined as a function of ![]() , in such a fashion that
the interaction of the methyl group of alanine with the rest of
the protein is effective at the beginning of the simulation,
i.e.
, in such a fashion that
the interaction of the methyl group of alanine with the rest of
the protein is effective at the beginning of the simulation,
i.e.![]() = 0, while
the glycine C
= 0, while
the glycine C![]() hydrogen does not interact with the rest
of the protein, and vice versa at the end of the
simulation, i.e.
hydrogen does not interact with the rest
of the protein, and vice versa at the end of the
simulation, i.e.![]() = 1.
For intermediate values of
= 1.
For intermediate values of ![]() , both the alanine and the glycine
side chains participate in non-bonded interactions with the rest
of the protein, scaled on the basis of the current value of
, both the alanine and the glycine
side chains participate in non-bonded interactions with the rest
of the protein, scaled on the basis of the current value of ![]() .
It should be emphasized that these side chains, however,
do not interact with themselves.
It is not necessary to explicitly exclude those atoms that are created
from those that will be annihilated in the course of the
FEP calculation.
.
It should be emphasized that these side chains, however,
do not interact with themselves.
It is not necessary to explicitly exclude those atoms that are created
from those that will be annihilated in the course of the
FEP calculation.
It is also worth noting that the free energy calculation does not alter intramolecular potentials, i.e.bond stretch, valence angle deformation, torsions, etc..., during the simulation. In calculations targetted at the estimation of free energy differences between two states characterized by distinct environments -- e.g.a ligand, bound to a protein in the first simulation, and solvated in water, in the second -- as is the case for most free energy calculations that make use of a thermodynamic cycle, perturbation of intramolecular terms can be safely avoided. [5]
The procedure implemented in NAMD is particularly
adapted for performing free
energy calculations that split the ![]() reaction path into a number of non-physical,
intermediate states, or ``windows''. Seperate simulations
can be started for each window.
Alternatively, the Tcl scripting ability of
NAMD can be employed advantageously
to perform the complete simulation in a single run.
An example making use of such script is supplied at the end
of this user guide.
reaction path into a number of non-physical,
intermediate states, or ``windows''. Seperate simulations
can be started for each window.
Alternatively, the Tcl scripting ability of
NAMD can be employed advantageously
to perform the complete simulation in a single run.
An example making use of such script is supplied at the end
of this user guide.
The following keywords can be used to control the alchemical free energy calculations.
The first example illustrates the use of Tcl scripting for running the alchemical FEP feature of NAMD:
fep on
fepfile ion.fep
fepCol X
fepOutfile ion.fepout
fepOutFreq 5
fepEquilSteps 5000
set step 0.0
set dstep 0.1
while {$step <= 0.9} {
lambda $step
lambda2 [expr $step+$dstep]
run 10000
set step [expr $step+$dstep]
}
Here, the pdb file read by NAMD to retrieve the information
about perturbed atoms is biotin.fep. The pertinent information
is present in the X column. The output file of the free energy
calculation is biotinr.fepout, in which energies are written
every 5 steps.
![]() , the width of the windows, is set to 0.1.
5000 MD steps are performed in each window to
equilibrate the system. In this particular instance,
the current value of
, the width of the windows, is set to 0.1.
5000 MD steps are performed in each window to
equilibrate the system. In this particular instance,
the current value of ![]() is controlled by the syntax set step.
The FEP calculation is run until
is controlled by the syntax set step.
The FEP calculation is run until ![]() reaches the
value 0.9. In every window, 10000 MD steps
are being performed.
reaches the
value 0.9. In every window, 10000 MD steps
are being performed.
In the second example, each ![]() -state is declared
explicitly, avoiding the use of Tcl scripting:
-state is declared
explicitly, avoiding the use of Tcl scripting:
fep on fepfile ion.fep fepCol X fepOutfile ion.fepout fepOutFreq 5 fepEquilSteps 5000 lambda 0.0 lambda2 0.1 run 10000 lambda 0.1 lambda2 0.2 run 10000
lambda 0.8 lambda2 0.9 run 10000 lambda 0.9 lambda2 1.0 run 10000
The FEP calculation is carried out from ![]() = 0.0 to
0.9. In each new window, 10000 MD steps are performed.
= 0.0 to
0.9. In each new window, 10000 MD steps are performed.
The fepOutFile contains electrostatic and van der Waals energy
data calculated for ![]() and
and ![]() , written every
fepOutFreq steps. The column dE is the energy
difference of the single configuration, dE_avg and dG
are the instantaneous ensemble average of the energy and the calculated
free energy at the time step specified in column 2, respectively.
The temperature is specified in the penultimate column. On completion
of fepEquilSteps steps, the calculation of dE_avg and
dG is restarted. The accumulated net free energy change is output
and the end of the simulation at each lambda value. The cummulative
average energy dE_avg value may be summed using the
trapezoidal rule to obtain an approximate TI estimate for the free
energy change during the run.
, written every
fepOutFreq steps. The column dE is the energy
difference of the single configuration, dE_avg and dG
are the instantaneous ensemble average of the energy and the calculated
free energy at the time step specified in column 2, respectively.
The temperature is specified in the penultimate column. On completion
of fepEquilSteps steps, the calculation of dE_avg and
dG is restarted. The accumulated net free energy change is output
and the end of the simulation at each lambda value. The cummulative
average energy dE_avg value may be summed using the
trapezoidal rule to obtain an approximate TI estimate for the free
energy change during the run.