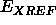 . The selection of the target is
specified by the TARGet keyword. There are seven possible
choices: RESIdual, AB, F1F1, F2F2, E1E1, E2E2, and PACKing.
. The selection of the target is
specified by the TARGet keyword. There are seven possible
choices: RESIdual, AB, F1F1, F2F2, E1E1, E2E2, and PACKing.
X-PLOR provides several possibilities for the
effective energy 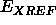 . The selection of the target is
specified by the TARGet keyword. There are seven possible
choices: RESIdual, AB, F1F1, F2F2, E1E1, E2E2, and PACKing.
. The selection of the target is
specified by the TARGet keyword. There are seven possible
choices: RESIdual, AB, F1F1, F2F2, E1E1, E2E2, and PACKing.
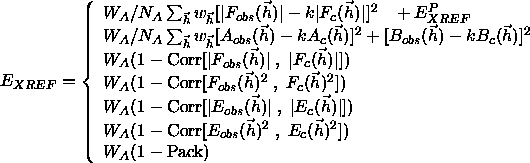
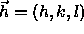 is the Miller indices of the
selected
reflections,
is the Miller indices of the
selected
reflections, 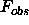 is the observed structure factors ,
is the observed structure factors ,
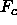 is the
computed structure factors,
is the
computed structure factors, 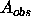 and
and 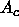 are the real components,
are the real components, 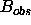 and
and 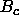 are
the imaginary components
of the structure factors,
are
the imaginary components
of the structure factors, 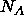 is a normalization factor,
k is a scale factor,
is a normalization factor,
k is a scale factor, 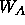 is an overall weight,
is an overall weight,
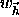 is the individual weights of the reflections,
Es are normalized structure factors,
and ``Corr" is the standard linear correlation
coefficient .
The computation of the
effective energy
is the individual weights of the reflections,
Es are normalized structure factors,
and ``Corr" is the standard linear correlation
coefficient .
The computation of the
effective energy 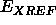 is accompanied by printing the
unweighted R value
is accompanied by printing the
unweighted R value
for the first choice in Eq. 12.1, the unweighted vector R value
for the second choice, or the various correlation coefficients for the third to sixth choices. The R values are stored in the symbol $R, and the correlation coefficients are stored in the symbol $CORR. If the data are partitioned into a test and a working set (see Chapter 15), the corresponding values for the test set are stored in the symbols $TEST R and $TEST CORR.
The selection of reflections is accomplished by the RESOlution and FWINdow statements (see below). ``Corr" is defined through
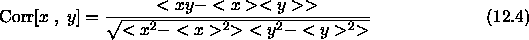
where the angle brackets denote a weighted (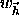 )
averaging over all
selected Miller indices
)
averaging over all
selected Miller indices 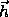 .
.
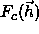 is defined as
is defined as

where 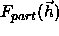 is ``partial" structure factors
that can be used
to represent a ``frozen" part of the molecule or bulk solvent
contributions, and
is ``partial" structure factors
that can be used
to represent a ``frozen" part of the molecule or bulk solvent
contributions, and
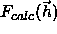 represents the structure factors that
are computed from the current atomic model.
represents the structure factors that
are computed from the current atomic model.
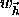 provides individual weights for
each reflection
provides individual weights for
each reflection 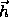 .
The overall weight
.
The overall weight 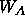 relates
relates 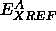 to the
other energy terms (see Section 4.6).
to the
other energy terms (see Section 4.6).
The normalized structure factors (Es) are computed from the structure factors (Fs) by averaging the Fs in equal reciprocal volume shells within the specified resolution limits. The number of shells is specified by MBINs.
The purpose of the normalization factor
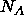 (first and second choice in Eq. 12.1)
is to make the weight
(first and second choice in Eq. 12.1)
is to make the weight 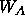 approximately independent of the resolution
range during SA-refinement.
approximately independent of the resolution
range during SA-refinement. 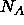 has been set to
has been set to
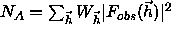 .
The scale
factor k in Eq. 12.1 is set to
.
The scale
factor k in Eq. 12.1 is set to
unless it is set manually by the FFK statement. Eq. 12.6 is a necessary condition to minimize the residual.
The term 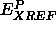 represents phase restraints
if
represents phase restraints
if 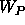 is set
to a nonzero number.
is set
to a nonzero number.
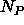 is a normalization factor set equal to the number of phase
specifications occurring in the sum,
is a normalization factor set equal to the number of phase
specifications occurring in the sum, 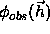 is the
phase centroid
obtained from mir or other methods (PHASe specifications;
see Section 12.4),
is the
phase centroid
obtained from mir or other methods (PHASe specifications;
see Section 12.4), 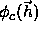 is the phase
of the calculated structure factors
is the phase
of the calculated structure factors 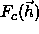 ,
,
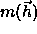 is the individual figure of
merit
(FOM specifications; see Section 12.4),
and
is the individual figure of
merit
(FOM specifications; see Section 12.4),
and 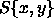 is a well function with harmonic
``wells" given by
is a well function with harmonic
``wells" given by
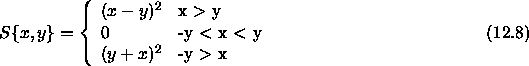
This form of the effective energy  ensures that the
calculated phases are restrained to
ensures that the
calculated phases are restrained to
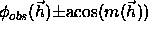 .
.
The structure factors (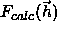 ) of the atomic model
are given by
) of the atomic model
are given by
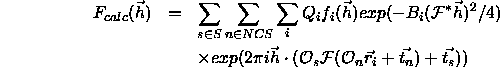
The first sum extends over all symmetry operators
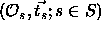 composed of the matrix
composed of the matrix  representing a rotation and a vector
representing a rotation and a vector  representing a translation.
The second sum extends over all non-crystallographic symmetry operators
representing a translation.
The second sum extends over all non-crystallographic symmetry operators
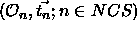 if they are present; otherwise only the identity transformation is
used (see Chapter 16).
The third sum extends over all unique atoms i of the system.
The quantity
if they are present; otherwise only the identity transformation is
used (see Chapter 16).
The third sum extends over all unique atoms i of the system.
The quantity 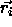 denotes the orthogonal coordinates of atom i
in Å.
denotes the orthogonal coordinates of atom i
in Å. 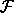 is the 3
is the 3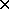 3 matrix that converts orthogonal
coordinates into
fractional coordinates;
3 matrix that converts orthogonal
coordinates into
fractional coordinates; 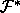 denotes the transpose of it.
The columns of
denotes the transpose of it.
The columns of 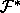 are equal to the reciprocal unit cell vectors
are equal to the reciprocal unit cell vectors
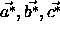 .
. 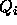 is the occupancy for each atom.
is the occupancy for each atom.
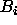 is the individual atomic temperature factor for atom i.
Both quantities correspond to the Q and B atom properties
(Section 2.16), which can be read along with the
atomic coordinates (see Section 6.1).
The atomic scattering factors
is the individual atomic temperature factor for atom i.
Both quantities correspond to the Q and B atom properties
(Section 2.16), which can be read along with the
atomic coordinates (see Section 6.1).
The atomic scattering factors 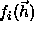 are approximated by an
expression consisting of four Gaussians and a constant
are approximated by an
expression consisting of four Gaussians and a constant
The constants 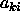 and
and 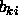 are specified in the SCATter
statement
and can be obtained from the International
Tables for Crystallography (Hahn ed. 1987).
The term
are specified in the SCATter
statement
and can be obtained from the International
Tables for Crystallography (Hahn ed. 1987).
The term
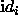 denotes an imaginary constant that can be
used to model anomalous
scattering.
Eq. 12.9
represents the space-group general form of the ``direct summation" formula,
which is used to
compute the structure factors. The fast Fourier transformation
(FFT) method consists of computing
denotes an imaginary constant that can be
used to model anomalous
scattering.
Eq. 12.9
represents the space-group general form of the ``direct summation" formula,
which is used to
compute the structure factors. The fast Fourier transformation
(FFT) method consists of computing
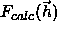 by
numerical evaluation of the atomic electron density on a finite grid
followed by an FFT. The FFT method provides a way to
speed up the calculation. The METHod statement can be used to
switch between the FFT method and the direct summation method.
by
numerical evaluation of the atomic electron density on a finite grid
followed by an FFT. The FFT method provides a way to
speed up the calculation. The METHod statement can be used to
switch between the FFT method and the direct summation method.
An approximation is used to reduce the computational requirements when
multiple evaluations of Eq. 12.1 are required.
The approximation involves not computing 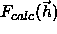 and its
first derivatives at every dynamics or minimization step. The first
derivatives are kept constant until any atom has moved by more than
and its
first derivatives at every dynamics or minimization step. The first
derivatives are kept constant until any atom has moved by more than
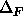 (TOLErance in xrefin statement)
relative to the position at which the derivatives were last
computed. At that point, all derivatives are updated. Typically,
(TOLErance in xrefin statement)
relative to the position at which the derivatives were last
computed. At that point, all derivatives are updated. Typically,
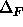 is set to 0.2 Å for dynamics
and to 0--0.05 Å for minimization.
is set to 0.2 Å for dynamics
and to 0--0.05 Å for minimization.
The PACKing target
is defined for evaluating the likelihood of
packing arrangements of the search model and its symmetry mates in the
crystal (Hendrickson and Ward 1976).
A finite grid that
covers the unit cell of the crystal is generated. The grid
size is specified through the GRID parameter in the
xrefin FFT statement.
All grid points
are marked that are within
the van der Waals radii around any atom of the search model and its
symmetry mates. The number of marked grid points
represents the union of the molecular spaces of the search model
and its symmetry mates. Maximization of the union of molecular
spaces is equivalent to minimization of the overlap. Thus,
an optimally packed structure has a maximum of the packing
function. ``Pack" in Eq. 12.1
contains the ratio of the number of marked
grid points to the total number of grid points in the unit cell.
For instance, a value of 0.6 means 40% solvent contents.
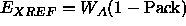 is then set to 0.4 if
is then set to 0.4 if 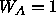 .
.
For further reading on the crystallographic target functions in X-PLOR, see Brünger (1988, 1989, 1990).