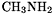 using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate.
using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate.
Overview of the Object-Oriented Input
MPQC starts off by creating a ParsedKeyVal object that parses the input file specified on the command line. The format of the input file is documented in The KeyVal Library. It is basically a free format input that associates keywords and logical groupings of keywords with values. The values can be scalars, arrays, or objects.
The keywords recognized by MPQC begin with the mpqc prefix. That is, they must be nested between an mpqc:( and a ). Alternately, each keyword can be individually prefixed by mpqc:. The primary keywords are given below. Some of the keywords specify objects, in which case the object will require more ParsedKeyVal input. These objects are created from the input by using their ParsedKeyVal constructors. These constructors are documented with the source code documentation for the class.
mole
opt
freq
thread
checkpoint.ckpt. The default is to checkpoint.
savestate.wfn. The default is to save state.
restart
restart_file.wfn the MolecularEnergy object will be restored. Otherwise, the Optimize object will be restored. The default file name is formed by appending .ckpt to the input file name with the extension removed.
do_energy
do_gradient
optimize
write_pdb
filename
print_timings
There are also some utility keywords that tell mpqc some technical details about how to do the calculation:
debugmatrixkit
A Walk-Through of an Object-Oriented Input File
This example input does a Hartree-Fock calculation on water. Following is the entire input, followed by a breakdown with descriptions.
% This input does a Hartree-Fock calculation on water.
molecule<Molecule>: (
symmetry = C2V
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
)
)
We start with a descriptive comment. Comments begin with a %. Everything from the % to the end of the line is ignored.
% This input does a Hartree-Fock calculation on water.
Now lets set up a Molecule object. The name of the object comes first, it is molecule. Then, in angle brackets, comes the type of the molecule, which is the class Molecule. The keyword and class name are followed by a : and then several pieces of input grouped between a pair of matching parentheses. These parentheses contain the information that will be given to Molecule KeyVal constructor.
molecule<Molecule>: (
The point group of the molecule is needed. This is done by assigning symmetry to a case insensitive Schoenflies symbol that is used to initialize a PointGroup object. An Abelian point group should be used.
symmetry = C2V
The default unit for the Cartesian coordinates is Bohr. You can specify other units by assigned unit to a string that will be used to initialize a Units object.
unit = angstrom
Finally, the atoms and coordinates are given. This can be given in the shorthand table syntax shown below. The headings of the table are the keywords between the first pair of brackets. These are followed by an = and another pair of brackets that contain the data. The first datum is assigned to the first element of the array that corresponds to the first heading, atom. The second datum is assigned to the first element of the array associated with the second heading, geometry, and so on. Here the second datum is actually a vector: the x, y and z coordinates of the first atom.
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
Next, a basis set object is given.
basis<GaussianBasisSet>: ( name = "STO-3G" molecule = $:molecule )
Now we will give the main body of input. All the subsequent keywords will be grouped in the mpqc section of the input (that is, each keyword will be prefixed with mpqc:).
mpqc: (
Next we give the mole keyword which provides a specialization of the MolecularEnergy class. In this case we will do a closed-shell Hartree-Fock calculation. That is done with an object of type CLHF. The keywords that CLHF accepts are given with the documentation for the CLHF class, usually in the description of the const RefKeyVal& constructor for the class. Also with the CLHF documentation is a list of parent classes. Each of the parent classes may also have input. This input is included with the rest of the input for the child class.
mole<CLHF>: (
The next line specifies the molecule to be used. There are two things to note, first that this is actually a reference to complete molecule specification elsewhere in the input file. The $ indicates that this is a reference and the keyword following the $ is the actual location of the molecule. The : in front of the keyword means that the keyword is not relative to the current location in the input, but rather relative to the root of the tree of keywords. Thus, this line grabs the molecule that was specified above. The molecule object could have been placed here, but frequently it is necessary that several objects refer to the exact same object and this can only be done using references.
The second point is that if you look at the documentation for CLHF, you will see that it doesn't read molecule keyword. However, if you follow its parent classes up to MolecularEnergy, you'll find that molecule is indeed read.
molecule = $:molecule
Just as we gave molecule, specify the basis set with the basis keyword as follows:
basis = $:basis
Now we close off the parentheses we opened above and we are finished.
) )
Sample Object-Oriented Input Files
The easiest way to get started with mpqc is to start with one of sample inputs that most nearly matches your problem. All of the samples inputs shown here can be found in the directory src/bin/mpqc/samples.
The following input will compute the Hartree-Fock energy of water.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C2V
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
memory = 16000000
)
)
The following input will compute the MP2 energy of water.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C2V
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% method for computing the molecule's energy
mole<MBPT2>: (
molecule = $:molecule
basis = $:basis
memory = 16000000
% reference wavefunction
reference<CLHF>: (
molecule = $:molecule
basis = $:basis
memory = 16000000
)
)
)
The following input will optimize the geometry of water using the quasi-Newton method.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C2V
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "6-31G*"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
)
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
)
% optimizer object for the molecular geometry
opt<QNewtonOpt>: (
function = $..:mole
update<BFGSUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
Optimization with a Computed Guess Hessian
The following input will optimize the geometry of water using the quasi-Newton method. The guess Hessian will be computed at a lower level of theory.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C2V
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.37000000 ]
H [ 0.78000000 0.00000000 -0.18000000 ]
H [ -0.78000000 0.00000000 -0.18000000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "6-31G*"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
)
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
guess_hessian<FinDispMolecularHessian>: (
molecule = $:molecule
only_totally_symmetric = yes
eliminate_cubic_terms = no
checkpoint = no
energy<CLHF>: (
molecule = $:molecule
memory = 16000000
basis<GaussianBasisSet>: (
name = "3-21G"
molecule = $:molecule
)
)
)
)
% optimizer object for the molecular geometry
opt<QNewtonOpt>: (
function = $..:mole
update<BFGSUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
Optimization Using Newton's Method
The following input will optimize the geometry of water using the Newton's method. The Hessian will be computed at each step in the optimization. However, Hessian recomputation is usually not worth the cost; try using the computed Hessian as a guess Hessian for a quasi-Newton method before resorting to a Newton optimization.
% Emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = c2v
unit = angstrom
{ atoms geometry } = {
O [ 0.00000000 0.00000000 0.36937294 ]
H [ 0.78397590 0.00000000 -0.18468647 ]
H [ -0.78397590 0.00000000 -0.18468647 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "3-21G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
restart = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
)
do_energy = no
do_gradient = no
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
memory = 16000000
coor = $..:coor
guess_wavefunction<CLHF>: (
molecule = $:molecule
total_charge = 0
basis<GaussianBasisSet>: (
molecule = $:molecule
name = "STO-3G"
)
memory = 16000000
)
hessian<FinDispMolecularHessian>: (
only_totally_symmetric = yes
eliminate_cubic_terms = no
checkpoint = no
)
)
optimize = yes
% optimizer object for the molecular geometry
opt<NewtonOpt>: (
print_hessian = yes
max_iterations = 20
function = $..:mole
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
The following input will compute Hartree-Fock frequencies by finite displacements. A thermodynamic analysis will also be performed. If optimization input is also provided, then the optimization will be run first, then the frequencies.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C1
{ atoms geometry } = {
O [ 0.0000000000 0.0000000000 0.8072934188 ]
H [ 1.4325589285 0.0000000000 -0.3941980761 ]
H [ -1.4325589285 0.0000000000 -0.3941980761 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
memory = 16000000
)
% vibrational frequency input
freq<MolecularFrequencies>: (
molecule = $:molecule
)
)
Giving Coordinates and a Guess Hessian
The following example shows several features that are really independent. The variable coordinates are explicitly given, rather than generated automatically. This is especially useful when a guess Hessian is to be provided, as it is here. This Hessian, as given by the user, is not complete and the QNewtonOpt object will fill in the missing values using a guess the Hessian provided by the MolecularEnergy object. Also, fixed coordinates are given in this sample input.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C1
{ atoms geometry } = {
H [ 0.088 2.006 1.438 ]
O [ 0.123 3.193 0.000 ]
H [ 0.088 2.006 -1.438 ]
O [ 4.502 5.955 -0.000 ]
H [ 2.917 4.963 -0.000 ]
H [ 3.812 7.691 -0.000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
)
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
extra_bonds = [ 2 5 ]
)
% use these instead of generated coordinates
variable<SetIntCoor>: [
<StreSimpleCo>:( atoms = [ 2 5 ] )
<BendSimpleCo>:( atoms = [ 2 5 4 ] )
<OutSimpleCo>: ( atoms = [ 5 2 1 3 ] )
<SumIntCoor>: (
coor: [
<StreSimpleCo>:( atoms = [ 1 2 ] )
<StreSimpleCo>:( atoms = [ 2 3 ] )
]
coef = [ 1.0 1.0 ]
)
<SumIntCoor>: (
coor: [
<StreSimpleCo>:( atoms = [ 4 5 ] )
<StreSimpleCo>:( atoms = [ 4 6 ] )
]
coef = [ 1.0 1.0 ]
)
<BendSimpleCo>:( atoms = [ 1 2 3 ] )
<BendSimpleCo>:( atoms = [ 5 4 6 ] )
]
% these are fixed by symmetry anyway,
fixed<SetIntCoor>: [
<SumIntCoor>: (
coor: [
<StreSimpleCo>:( atoms = [ 1 2 ] )
<StreSimpleCo>:( atoms = [ 2 3 ] )
]
coef = [ 1.0 -1.0 ]
)
<SumIntCoor>: (
coor: [
<StreSimpleCo>:( atoms = [ 4 5 ] )
<StreSimpleCo>:( atoms = [ 4 6 ] )
]
coef = [ 1.0 -1.0 ]
)
<TorsSimpleCo>:( atoms = [ 2 5 4 6] )
<OutSimpleCo>:( atoms = [ 3 2 6 4 ] )
<OutSimpleCo>:( atoms = [ 1 2 6 4 ] )
]
)
% optimizer object for the molecular geometry
opt<QNewtonOpt>: (
function = $..:mole
update<BFGSUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
% give a partial guess hessian in internal coordinates
% the missing elements will be filled in automatically
hessian = [
[ 0.0109261670 ]
[ -0.0004214845 0.0102746106 ]
[ -0.0008600592 0.0030051330 0.0043149957 ]
[ 0.0 0.0 0.0 ]
[ 0.0 0.0 0.0 ]
[ 0.0 0.0 0.0 ]
[ 0.0 0.0 0.0 ]
]
)
)
Optimization with a Hydrogen Bond
The automatic internal coordinate generator will fail if it cannot find enough redundant internal coordinates. In this case, the internal coordinate generator must be explicitly created in the input and given extra connectivity information, as is shown below.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = C1
{ atoms geometry } = {
H [ 0.088 2.006 1.438 ]
O [ 0.123 3.193 0.000 ]
H [ 0.088 2.006 -1.438 ]
O [ 4.502 5.955 -0.000 ]
H [ 2.917 4.963 -0.000 ]
H [ 3.812 7.691 -0.000 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "STO-3G"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
)
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
% give an internal coordinate generator that knows about the
% hydrogen bond between atoms 2 and 5
generator<IntCoorGen>: (
molecule = $:molecule
extra_bonds = [ 2 5 ]
)
)
% optimizer object for the molecular geometry
opt<QNewtonOpt>: (
function = $..:mole
update<BFGSUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
This example shows how to selectively fix internal coordinates in an optimization. Any number of linearly independent coordinates can be given. These coordinates must remain linearly independent throughout the optimization, a condition that might not hold since the coordinates can be nonlinear.
By default, the initial fixed coordinates' values are taken from the cartesian geometry given by the Molecule object; however, the molecule will be displaced to the internal coordinate values given with the fixed internal coordinates if have_fixed_values keyword is set to true, as shown in this example. In this case, the initial cartesian geometry should be reasonably close to the desired initial geometry and all of the variable coordinates will be frozen to their original values during the initial displacement.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = CS
{ atoms geometry } = {
H [ 3.04 -0.69 -1.59 ]
H [ 3.04 -0.69 1.59 ]
N [ 2.09 -0.48 -0.00 ]
C [ -0.58 -0.15 0.00 ]
H [ -1.17 1.82 0.00 ]
H [ -1.41 -1.04 -1.64 ]
H [ -1.41 -1.04 1.64 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "4-31G*"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
have_fixed_values = yes
fixed<SetIntCoor>: [
<OutSimpleCo>: ( value = -0.1
label = "N-inversion"
atoms = [4 3 2 1] )
]
)
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
)
% optimizer object for the molecular geometry
opt<QNewtonOpt>: (
max_iterations = 20
function = $..:mole
update<BFGSUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
This example shows a transition state optimization of the N-inversion in 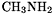 using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate.
using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = CS
{ atoms geometry } = {
H [ 3.045436 -0.697438 -1.596748 ]
H [ 3.045436 -0.697438 1.596748 ]
N [ 2.098157 -0.482779 -0.000000 ]
C [ -0.582616 -0.151798 0.000000 ]
H [ -1.171620 1.822306 0.000000 ]
H [ -1.417337 -1.042238 -1.647529 ]
H [ -1.417337 -1.042238 1.647529 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "4-31G*"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
followed<OutSimpleCo> = [ "N-inversion" 4 3 2 1 ]
)
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
)
% optimizer object for the molecular geometry
opt<EFCOpt>: (
transition_state = yes
mode_following = yes
max_iterations = 20
function = $..:mole
update<PowellUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)
Transition State Optimization with a Computed Guess Hessian
This example shows a transition state optimization of the N-inversion in 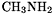 using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate. An approximate guess Hessian will be computed, which makes the optimiziation converge much faster in this case.
using mode following. The initial geometry was obtained by doing a few fixed coordinate optimizations along the inversion coordinate. An approximate guess Hessian will be computed, which makes the optimiziation converge much faster in this case.
% emacs should use -*- KeyVal -*- mode
% molecule specification
molecule<Molecule>: (
symmetry = CS
{ atoms geometry } = {
H [ 3.045436 -0.697438 -1.596748 ]
H [ 3.045436 -0.697438 1.596748 ]
N [ 2.098157 -0.482779 -0.000000 ]
C [ -0.582616 -0.151798 0.000000 ]
H [ -1.171620 1.822306 0.000000 ]
H [ -1.417337 -1.042238 -1.647529 ]
H [ -1.417337 -1.042238 1.647529 ]
}
)
% basis set specification
basis<GaussianBasisSet>: (
name = "4-31G*"
molecule = $:molecule
)
mpqc: (
checkpoint = no
savestate = no
% molecular coordinates for optimization
coor<SymmMolecularCoor>: (
molecule = $:molecule
generator<IntCoorGen>: (
molecule = $:molecule
)
followed<OutSimpleCo> = [ "N-inversion" 4 3 2 1 ]
)
% method for computing the molecule's energy
mole<CLHF>: (
molecule = $:molecule
basis = $:basis
coor = $..:coor
memory = 16000000
guess_hessian<FinDispMolecularHessian>: (
molecule = $:molecule
only_totally_symmetric = yes
eliminate_cubic_terms = no
checkpoint = no
energy<CLHF>: (
molecule = $:molecule
memory = 16000000
basis<GaussianBasisSet>: (
name = "3-21G"
molecule = $:molecule
)
)
)
)
% optimizer object for the molecular geometry
opt<EFCOpt>: (
transition_state = yes
mode_following = yes
max_iterations = 20
function = $..:mole
update<PowellUpdate>: ()
convergence<MolEnergyConvergence>: (
cartesian = yes
energy = $..:..:mole
)
)
)